Thermal Systems Part 1

Question 1: How does the cooling behavior change if we vary the parameters and C? Figure this out using intuition and the above equations, and then vary these parameters in your program to confirm your conclusions.

dE = -((T - Tair) / Rth) * dt
dT = dE / C
T = T + dT

Based off the the above equations, I expected an increase in Rth to decrease (the absolute value of) dE and therefore decrease dT, which means the cooling would be slower. A decrease in Rth would increase dE and therefore increase dT, whch means the cooling would be faster. An increase in C would decrease dT and therefore cooling would be slower. An decrease in C would increase dT and therefore cooling would be faster.

Below is a picture of the code for which we manipulated the values of Rth and C and pictures of the resulting graphs.

                       

Rth = 85

Cooling occurs slowly, as expected.

R = 0.085

Cooling occurs quickly, as expected. 

C = 10

Cooling occurs quickly, as expected.

C = 100,000

Cooling occurs slowly, as expected.

Add a heater

Now let’s explore what happens if we add a heater to the pot. Suppose the coffee starts out at room temperature (273 K) and we turn on a heating element that adds thermal energy to the system at a constant rate P. In this case we expect that:

Question 2: Calculate a good value for P if we want our coffee to heat up to the Starbucks ideal 84°C, using the Rth from the MATLAB script?

The easiest way to do this is to look at the equation right after the heater is turned on, at time 0. If we divide the above equation by dt, set it equal to zero and solve for P, we get P = (T-Tair)/Rth, which simplifies to 64/0.85, which is about 75 J/s. 

 We can find Rth by arranging the equation from the last question. Rth = (T - Tair)/P = (353 - 293) K / 75 W = 0.8 K/W. 

Since dT/dt = P/C at t = 0, we can find the slope of the graph where it is approximately linear, from about 0 to 250s. The slope is about (310-300)K/(250-0)s = 0.08 K/s. 

We can then estimate C as C = P/(dT/dt) = 75 W / 0.08 K/s = about 938 J/K. This is pretty close to the given answer of 1000 J/K, and it probably differs due to the estimations made from reading the graph. 

Question 3) Modify the above programs to simulate a temperature controller that uses bang-bang control to reach and maintain the desired temperature. Bang-bang control is a very common approach for thermostats. Why is bang-bang control appropriate for many thermal systems? When might it be insufficient?

We modified our code so that if the temperature of the coffee was less than the ideal 357 K, the heater would turn on at a full power of 200 Watts. If the coffee temperature was greater than or equal to 357 K, the heater would turn off. Here is our code and a picture of our resulting graph. 



   

As you can see on the graph, the temperature of the coffee fluctuates around 357 K as the heater turns on and off. Bang-bang control is ideal for thermal systems in which you want to get close to an ideal temperature, but precision isn't as important. However, for systems where a few Kelvin difference would have a big effect, it's not a good idea. For example, if someone picks up the coffee cup when it is at a max fluctuation, it could be 5 degrees Fahrenheit colder or hotter than they were expecting. This would be bad, especially if it was hotter, because they might burn their tongue.  

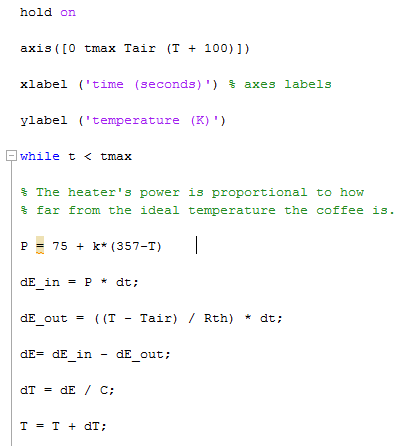
Question 4) Create a program that uses proportional control to reach and maintain the desired temperature. How does this approach compare to bang-bang control?

We edited our code so that the power of the heater changed according to how far the temperature of the coffee was from the ideal temperature. We experimented with several values of k and the initial constant and found that a k value of 20 and starting value of 75 K heated the coffee up the fastest and produced the smallest fluctuations from the ideal temperature.

         

             

Compared to bang-bang control, proportional control heats the coffee faster (200 seconds vs. 400 seconds to reach ideal temperature) and keeps it at the ideal temperature instead of fluctuating.

Question 5) Suppose there is a delay between the time the coffee reaches a given temperature and when the temperature sensor records that temperature. Modify both of your programs to include this effect. What is the impact of this “sensor delay” on your system in each case? What other delay(s) might you expect in your thermodynamic system, apart from sensor delays?

Proportional Control

       

         
         

       

There's a small bump at the beginning, but then the graph dampens out at a steady temperature. 

Bang-bang Control

         
           
           

When there's a delay with bang-bang control, the whole graph is affected instead of just the beginning (although I'm not sure if this is right). The temperature fluctuates between 350 K and 365 K, which is a much larger range than bang-bang without a delay. This shows that, especially when real-life issues like sensor delays are taken into consideration, proportional control is really important.

In addition to the temperature sensor delay, there might be a delay between when the heater is told to turn on/off and when it actually does.